
Mathcad evaluates the root function using the secant method. What to do when the root function does not converge Using a plot and the root function tofind roots of an expression. Type x: 3. Your choice of guess value determines which root Mathcad returns Mathcad uses this as a starting value in its search for a solution.įor example, to define a as the solution to the equation, follow these steps: You should assign a number to this variable before using the root function. It is this variable that Mathcad will vary to make the expression go to zero. The second argument is a variable name that appears in the expression. The first argument is either a function defined elsewhere in the worksheet, or an expression. Instruct the calculator to find the roots: SOLVE ( Function Key F). Both arguments to this function must be scalar. equation solvers in Excel and Mathcad when solving the same problems Sam- ple Prob. I have no idea what the symbolics thinks it is. Returns the value of z at which the expression or functionj(z) is equal to O. Basically polyroots is a function which should only be evaluated numerically. Once this is done, the function returns the value that makes the expression equal zero. It then varies that variable until the expression is equal to zero. This function takes an expression and one of the variables from the expression. To solve a single equation in a single unknown, use the root function.
Mathcad polyroots function how to#
How to use “solve blocks” to solve systems of n equations in n unknowns.Įxamples of how to solve systems of equations efficiently for various values of a parameter.

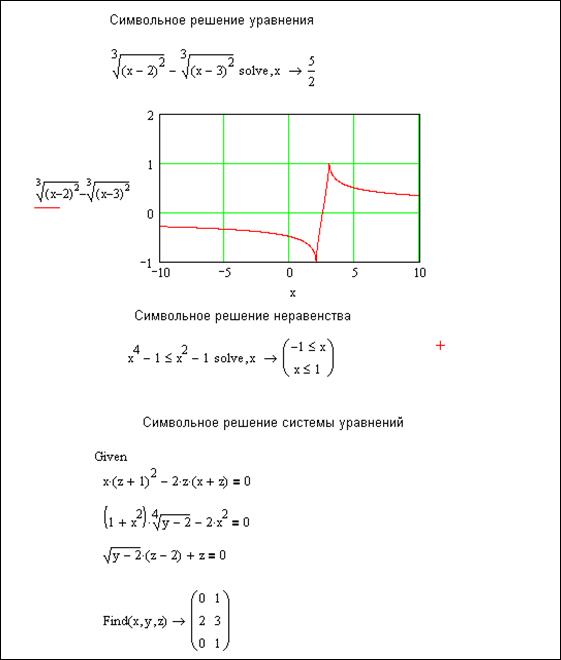
How to use Mathcad’s root function to numerically solve one equation in one unknown. This PTC Mathcad tutorial is the first part on the subject of Functions, and it covers how users can define their own custom functions.PTC Mathcad is enginee. Include all coefficients in the vector even if they are zero. In order to use this function, you need to create a vector of coefficients of the polynomial. The solution is returned in a vector containing the roots of the polynomial. The techniques described here generate numeric solutions.” Symbolic Calculation,” describes a variety of techniques for solving equations symbolically. The polyroots function is used to solve for all solutions to a polynomial equation at the same time. This chapter describes how to solve equations ranging from a singleĮquation in one unknown to systems of up to fifty equations in fifty unknowns.


 0 kommentar(er)
0 kommentar(er)
